Graphic Semiology Fundamentals

Introduction to Graphic Semiology

Graphic semiology studies how visual elements act as a language to encode, communicate, and process information. Pioneered by Jacques Bertin, it formalizes the grammar of graphics: how visual variables (symbols, signs, marks) represent data in diagrams, maps, and networks. Bertin’s thesis is that graphics constitute a system with its own syntax and semantics, much as in verbal language.

Sémiologie graphique by Jacques Bertin, EHESS 2013 reprint Source: Wikipedia | License: CC BY 4.0

1. Theoretical Foundations

1.1. Graphics as Language

Graphics are a visual code, and each constructed image is a message.
Visual elements (the signifiers) correspond to information components (the signified).
The goal is to achieve “visual unity,” maximizing both efficiency and global apprehension of a message.

1.2. Historical Evolution

Bertin's laboratory, the Laboratoire de Graphique, crystallized these principles through interdisciplinary collaboration, handling demands across social sciences, geography, and cartography.
The 1967 “Sémiologie graphique” was a paradigm shift, bringing a rational, systematic language for visual analytics.

1.3. An example from a research paper

This graph comes from the research paper: Different languages, similar encoding efficiency: Comparable information rates across the human communicative niche by Christophe Coupé, Yoon Mi Oh, Dan Dediu, and François Pellegrino.
Source: Science.org

1.4. [Optional] Information Rate (IR) Definition

In the graph below, "SR" stands for Speech Rate and "IR" stands for Information Rate.
Based on Shannon's information theory in the study:
- Information Density ($ID$): Average bits of information per syllable (conditional entropy, accounting for syllable dependencies).
- Speech Rate ($SR$): Syllables spoken per second.
$IR = ID \times SR$ (bits/second).
Across $17$ languages, $IR$ averages $\text{\textasciitilde} 39$ bits/s, showing languages encode info at similar rates despite differences in $ID$ or $SR$.

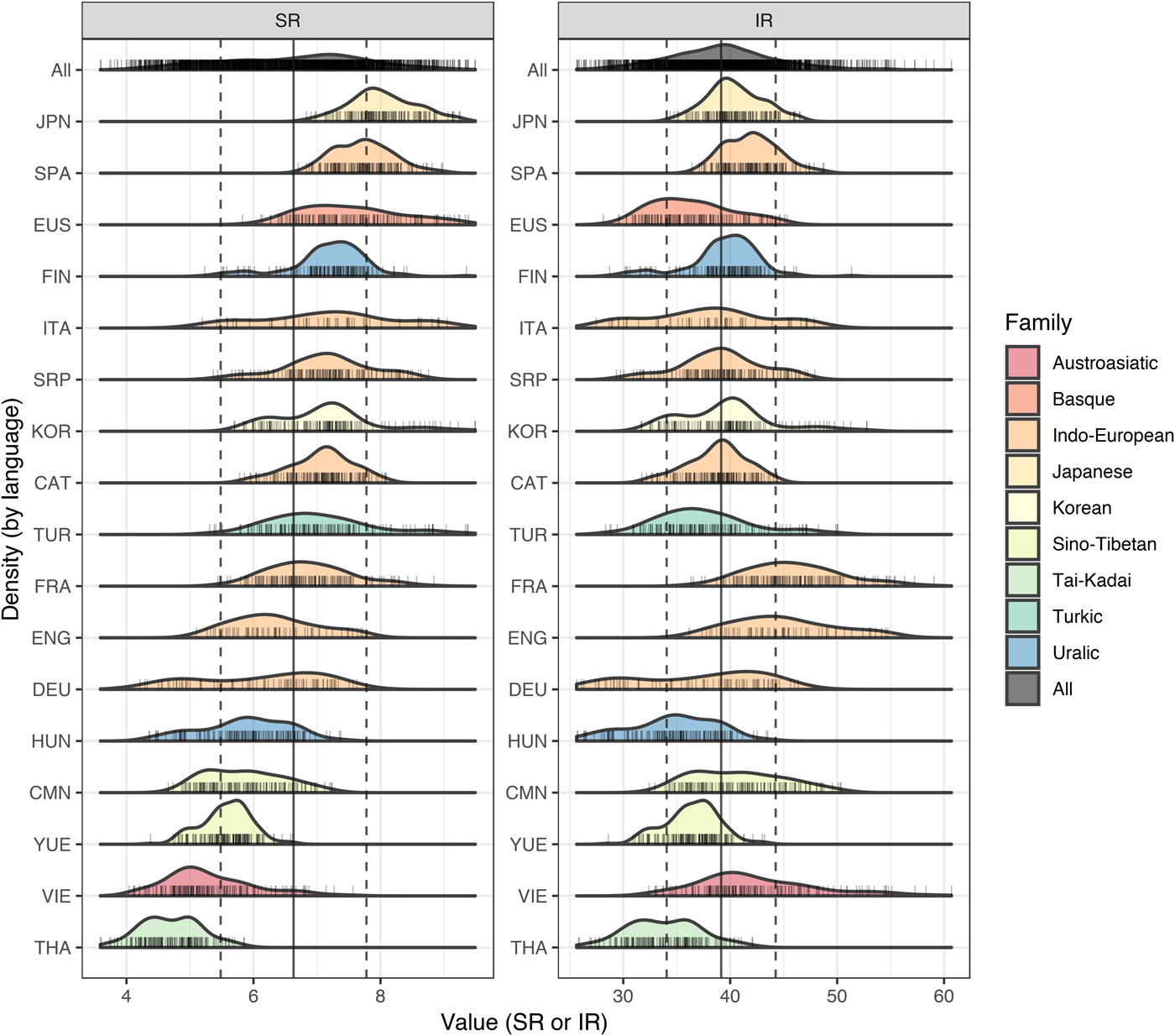
Different languages, similar encoding efficiency: Comparable information rates across the human communicative niche - by Christophe Coupé, Yoon Mi Oh, Dan Dediu, and François Pellegrino. Source: Science.org

More detailed explanations are available here: Computing Shannon Entropy for Information Density.

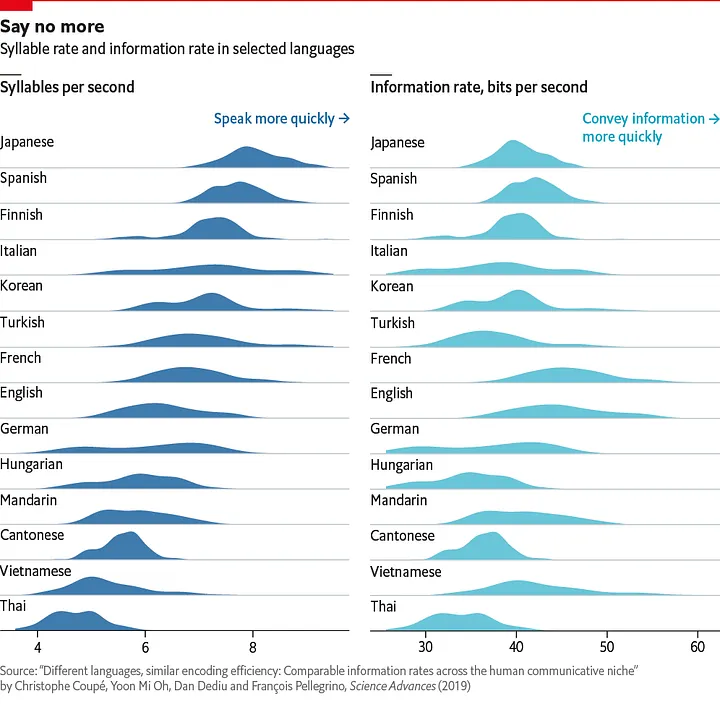
1.4. An adaptation from The Economist

This graph comes from the article: Why are some languages spoken faster than others? by The Economist (Sep 28th 2019). Link

Why are some languages spoken faster than others? by The Economist - Sep 28th 2019

1.5. Discussion

Looking at the two above graphs:

What are the signifiers ?
What are the signified ?
What can we conclude from those graphs ?
How do they compare in terms of visual unity?

2. Structure of Information

2.1. Theoretical Foundations

Invariant (Theme/Essence): The unifying core of the data (e.g., a common subject or theme linking all data points).
Components (Variables/Items): Distinct fields or characteristics in the dataset (nominal, ordinal, quantitative).
Components can relate differentially (qualitative categories), ordinally (rank/order), or quantitatively (measured scales).
Graphic System: Theoretical Framework
- The cartographic/graphic “plane” is the two-dimensional space in which elements are organized.
- It translates “plane geometry” into meaningful arrangements: quantities, categories, relationships, or spatial representations.
Classes of Representation
- Diagrams: Abstract data structures (e.g., time series, bar charts).
- Networks: Relationships among entities (e.g., graphs, flow diagrams).
- Maps: Spatial embedding of data (e.g., geographic maps).

2.2 Datasets used in the following examples

import matplotlib.pyplot as plt
import pandas as pd

# Raw data lists - all buildings over 500m
buildings = ['Burj Khalifa', 'Merdeka 118', 'Shanghai Tower', 'Abraj Al-Bait', 'Ping An']
heights = [828, 679, 632, 601, 599]  # meters
cities = ['Dubai', 'Kuala Lumpur', 'Shanghai', 'Mecca', 'Shenzhen']
completion_years = [2010, 2023, 2015, 2012, 2017]

# Create a DataFrame for better display
df = pd.DataFrame({
    'Building': buildings,
    'Height (m)': heights,
    'City': cities,
    'Completion Year': completion_years
})

# Sort by height for better visualization
df_sorted = df.sort_values('Height (m)', ascending=False).reset_index(drop=True)

# Create a clean table visualization
fig, ax = plt.subplots(figsize=(12, 8))
ax.axis('tight')
ax.axis('off')

# Create table
table = ax.table(cellText=df_sorted.values,
                colLabels=df_sorted.columns,
                cellLoc='center',
                loc='center',
                bbox=[0, 0.3, 1, 0.6])

# Style the table
table.auto_set_font_size(False)
table.set_fontsize(12)
table.scale(1, 2)

# Style header row
for i in range(len(df_sorted.columns)):
    table[(0, i)].set_facecolor('#4472C4')
    table[(0, i)].set_text_props(weight='bold', color='white')

# Style data rows with alternating colors
for i in range(1, len(df_sorted) + 1):
    for j in range(len(df_sorted.columns)):
        if i % 2 == 0:
            table[(i, j)].set_facecolor('#F2F2F2')
        else:
            table[(i, j)].set_facecolor('white')

# Add title and description
plt.title('DATASET: World\'s Tallest Buildings Over 500m\n' +
          'INVARIANT: Buildings | COMPONENTS: Name, Height, City, Year',
          fontsize=16, fontweight='bold', pad=20)

# Add summary statistics
plt.figtext(0.05, 0.15, 
           f"Dataset Summary:\n" +
           f"• Total buildings: {len(buildings)}\n" +
           f"• Height range: {min(heights)}m - {max(heights)}m\n" +
           f"• Year range: {min(completion_years)} - {max(completion_years)}\n" +
           f"• Average height: {sum(heights)/len(heights):.0f}m",
           fontsize=11, 
           bbox=dict(boxstyle="round,pad=0.5", facecolor="lightblue", alpha=0.3))

plt.figtext(0.35, 0.15,
           f"Data Types:\n" +
           f"• Building names: Nominal (categorical)\n" +
           f"• Heights: Quantitative (continuous)\n" +
           f"• Cities: Nominal (categorical)\n" +
           f"• Years: Quantitative (discrete)",
           fontsize=11,
           bbox=dict(boxstyle="round,pad=0.5", facecolor="lightgreen", alpha=0.3))

plt.tight_layout()
plt.show()

2.3. An example with a bar chart

import matplotlib.pyplot as plt

# Real data: World's tallest buildings over 500m
# INVARIANT: Buildings (the theme)

# Raw data lists - all buildings over 500m
buildings = ['Burj Khalifa', 'Merdeka 118', 'Shanghai Tower', 'Abraj Al-Bait', 'Ping An']
heights = [828, 679, 632, 601, 599]  # meters
cities = ['Dubai', 'Kuala Lumpur', 'Shanghai', 'Mecca', 'Shenzhen']
completion_years = [2010, 2023, 2015, 2012, 2017]

# Sort by year for proper x-axis
sorted_data = sorted(zip(completion_years, buildings, heights, cities))
years_sorted = [item[0] for item in sorted_data]
buildings_sorted = [item[1] for item in sorted_data]
heights_sorted = [item[2] for item in sorted_data]
cities_sorted = [item[3] for item in sorted_data]

# Create larger figure with high DPI
plt.figure(figsize=(16, 10), dpi=150)
colors = ['#2C3E50', '#34495E', '#5D6D7E', '#85929E', '#AEB6BF']  # Different shades of grey
bars = plt.bar(years_sorted, heights_sorted, width=1, color=colors, alpha=0.9, 
            edgecolor='black', linewidth=2)

# Add building names and cities above bars with bigger text and more space
for i, (bar, building, city) in enumerate(zip(bars, buildings_sorted, cities_sorted)):
    # Building name - bigger font and more spacing
    plt.text(bar.get_x() + bar.get_width()/2, bar.get_height() + 35, 
            building, ha='center', va='bottom', fontsize=16, fontweight='bold')
    # City name in italics - bigger font and more spacing
    plt.text(bar.get_x() + bar.get_width()/2, bar.get_height() + 65, 
            city, ha='center', va='bottom', fontsize=14, style='italic')

# X-axis with actual years as x values
all_years = list(range(2010, 2024))
plt.xticks(all_years, fontsize=16, rotation=45)
plt.xlabel('Completion Year', fontsize=16, fontweight='bold')
plt.ylabel('Height (meters)', fontsize=16, fontweight='bold')
plt.title('STRUCTURE: Invariant + Components\nInvariant: Buildings | Components: Name (nominal), Height (quantitative), City (nominal), Year (quantitative)', 
        fontsize=20, pad=30, fontweight='bold')

plt.ylim(0, max(heights_sorted) + 120)  # Extra space for larger labels

# Improve overall appearance
plt.grid(axis='y', alpha=0.3, linestyle='--')
plt.tight_layout()

plt.show()

2.4. 💬 Discussion

Looking at the above graph:

What are the signifiers ?
What are the signified ?
What can we conclude from those graphs ?
How do they compare in terms of readability and visual unity?

3. Relationships

3.1. Relations and dimensionality

Key in analysis: how components relate, not necessarily their individual meanings, but their differences and connections.
For every dataset, determining its dimensionality (number/nature of components) directs the choice of graphic strategy.

3.2. Datasets used in the following examples

100m men world record progression

Date	Time (s)	Athlete Country
1912-07-06	10.6	🇺🇸
1921-04-23	10.4	🇺🇸
1930-08-09	10.3	🇨🇦
1936-06-20	10.2	🇺🇸
1956-08-03	10.1	🇺🇸
1960-06-21	10.0	🇩🇪
1968-06-20	9.95	🇺🇸
1983-07-03	9.93	🇺🇸
1988-09-24	9.92	🇺🇸
1991-06-14	9.90	🇺🇸
1991-08-25	9.86	🇺🇸
1994-07-06	9.85	🇺🇸
1996-07-27	9.84	🇨🇦
1999-06-16	9.79	🇺🇸
2005-06-14	9.77	🇯🇲
2008-05-31	9.72	🇯🇲
2008-08-16	9.69	🇯🇲
2009-08-16	9.58	🇯🇲

Source: Wikipedia / World Athletics (as of September 2025)

North countries national development profiles

Country	GDP per Capita	Life Expectancy	Education Index	Happiness Score	Innovation Index	Environmental Score
Norway 🇳🇴	75	82	95	76	68	78
Switzerland 🇨🇭	81	84	88	75	67	81
Denmark 🇩🇰	60	81	92	78	58	78
Iceland 🇮🇸	52	83	95	75	55	68
Netherlands 🇳🇱	53	82	93	74	58	76
Sweden 🇸🇪	51	83	94	73	63	78
Germany 🇩🇪	46	81	93	70	87	77
Canada 🇨🇦	46	82	92	72	61	72
Australia 🇦🇺	55	83	92	73	46	60
Japan 🇯🇵	39	85	85	59	54	65
South Korea 🇰🇷	31	83	85	58	64	63
United Kingdom 🇬🇧	42	81	90	70	59	58
France 🇫🇷	40	83	88	66	54	80
Belgium 🇧🇪	47	82	89	69	50	73
Austria 🇦🇹	48	81	91	71	45	79

Source: United Nations Development Programme, World Bank, OECD, WIPO, and World Happiness Report, compiled and normalized (2024–2025)

3.3. An example with a scatter plot

Here we add a regression line to the scatter plot to show the trend of the data. It show how to combine lines and points in the same plot.

Look carefully at the axis: the $y$ axis is inverted, because the faster times are better. This is a common practice in data visualization, it's not mandatory, but it helps to make the plot more readable.

import matplotlib.pyplot as plt
import matplotlib.dates as mdates
from datetime import datetime
import numpy as np

# World record data (precise date, time, country)
records = [
    ("1912-07-06", 10.6, "USA", "🇺🇸"),
    ("1921-04-23", 10.4, "USA", "🇺🇸"),
    ("1930-08-09", 10.3, "CAN", "🇨🇦"),
    ("1936-06-20", 10.2, "USA", "🇺🇸"),
    ("1956-08-03", 10.1, "USA", "🇺🇸"),
    ("1960-06-21", 10.0, "GER", "🇩🇪"),
    ("1968-06-20", 9.95, "USA", "🇺🇸"),
    ("1983-07-03", 9.93, "USA", "🇺🇸"),
    ("1988-09-24", 9.92, "USA", "🇺🇸"),
    ("1991-06-14", 9.90, "USA", "🇺🇸"),
    ("1991-08-25", 9.86, "USA", "🇺🇸"),
    ("1994-07-06", 9.85, "USA", "🇺🇸"),
    ("1996-07-27", 9.84, "CAN", "🇨🇦"),
    ("1999-06-16", 9.79, "USA", "🇺🇸"),
    ("2005-06-14", 9.77, "JAM", "🇯🇲"),
    ("2008-05-31", 9.72, "JAM", "🇯🇲"),
    ("2008-08-16", 9.69, "JAM", "🇯🇲"),
    ("2009-08-16", 9.58, "JAM", "🇯🇲")
]

dates = [datetime.strptime(r[0], "%Y-%m-%d") for r in records]
times = [r[1] for r in records]
countries = [r[2] for r in records]
emojis = [r[3] for r in records]

colors = {"USA": "#1f77b4", "CAN": "#ff7f0e", "JAM": "#2ca02c", "GER":"#999999"}
point_colors = [colors[c] for c in countries]

plt.figure(figsize=(12, 7))
plt.scatter(dates, times, c=point_colors, s=85, edgecolor='black', label="World Record")

# Prepare dates for proper regression with zero-based normalization
x = mdates.date2num(dates)
x0 = x - x[0]

# Regression line on normalized x axis
z = np.polyfit(x0, times, 1)
p = np.poly1d(z)
plt.plot(dates, p(x0), "r--", alpha=0.8, linewidth=2, 
        label=f"Trend: {z[0]:.5f} s/day")

plt.xlabel('Date', fontsize=13)
plt.ylabel('Time (seconds)', fontsize=13)
plt.title(
    '100m Men World Record Progression\n'
    'Relationship: Athletic Performance vs Time\n'
    'Source: Wikipedia / World Athletics (as of September 2025)',
    fontsize=15,
    pad=18,
    fontweight='bold'
)
plt.gca().invert_yaxis()
plt.grid(True, alpha=0.3)

# Custom legend for countries (name + color + emoji)
from matplotlib.lines import Line2D
legend_elements = [
    Line2D([0], [0], marker='o', color='w', markerfacecolor=colors["USA"], 
        markeredgecolor='black', markersize=11, label='USA'),
    Line2D([0], [0], marker='o', color='w', markerfacecolor=colors["CAN"], 
        markeredgecolor='black', markersize=11, label='Canada'),
    Line2D([0], [0], marker='o', color='w', markerfacecolor=colors["JAM"],
        markeredgecolor='black', markersize=11, label='Jamaica'),
    Line2D([0], [0], marker='o', color='w', markerfacecolor=colors["GER"],
        markeredgecolor='black', markersize=11, label='Germany')
]
plt.legend(
    handles=legend_elements,
    loc='lower right',
    fontsize=13,
    title="Country"
)
plt.tight_layout()
plt.show()

Since not only has the 100m men world record, but also most world records (whatever the sport), been improved continuously during the last century, what can we conclude about the evolution in the field of athletics?

3.4. An example with a heatmap

This example demonstrates how multiple quantitative components relate across different entities. The heatmap reveals patterns, clusters, and trade-offs that emerge from multi-dimensional data without incorrectly connecting nominal categories.

The y-axis is sorted by GDP per capita, descending.

import matplotlib.pyplot as plt
import numpy as np

countries = ['Norway', 'Switzerland', 'Denmark', 'Iceland', 'Netherlands', 
            'Sweden', 'Germany', 'Canada', 'Australia', 'Japan', 'South Korea',
            'United Kingdom', 'France', 'Belgium', 'Austria']

data = {
    'GDP per Capita': [75, 81, 60, 52, 53, 51, 46, 46, 55, 39, 31, 42, 40, 47, 48],
    'Life Expectancy': [82, 84, 81, 83, 82, 83, 81, 82, 83, 85, 83, 81, 83, 82, 81],
    'Education Index': [95, 88, 92, 95, 93, 94, 93, 92, 92, 85, 85, 90, 88, 89, 91],
    'Happiness Score': [76, 75, 78, 75, 74, 73, 70, 72, 73, 59, 58, 70, 66, 69, 71],
    'Innovation Index': [68, 67, 58, 55, 58, 63, 87, 61, 46, 54, 64, 59, 54, 50, 45],
    'Environmental Score': [78, 81, 78, 68, 76, 78, 77, 72, 60, 65, 63, 58, 80, 73, 79]
}

data_matrix = np.array([data[key] for key in data.keys()]).T

# Sort countries by GDP per capita (descending)
sorted_indices = np.argsort(data['GDP per Capita'])[::-1]
countries_sorted = [countries[i] for i in sorted_indices]
data_matrix_sorted = data_matrix[sorted_indices]

fig, ax = plt.subplots(figsize=(12, 10))
im = ax.imshow(data_matrix_sorted, cmap='RdYlBu_r', aspect='auto', vmin=30, vmax=95)

for i in range(len(countries_sorted)):
    for j in range(len(data.keys())):
        val = int(data_matrix_sorted[i, j])
        color = 'black' if 50 <= val <= 80 else 'white'
        ax.text(j, i, val, ha='center', va='center', color=color, fontweight='bold')

ax.set_xticks(range(len(data.keys())))
ax.set_xticklabels(list(data.keys()), rotation=45, ha='right', fontsize=13)
ax.set_yticks(range(len(countries_sorted)))
ax.set_yticklabels(countries_sorted)

cbar = fig.colorbar(im, ax=ax)
cbar.set_label('Score', rotation=270, labelpad=15)

ax.set_title('DIMENSIONALITY: 6D Data Matrix\nInvariant: National Profiles | Each cell = one relationship', 
            fontsize=16, fontweight='bold', pad=25)
ax.set_xlabel('Components (Dimensions)', fontsize=14)
ax.set_ylabel('Countries (Entities)', fontsize=12)

plt.tight_layout()
plt.show()

3.5. Another example with a heatmap

import matplotlib.pyplot as plt
import numpy as np

data = {
    'GDP per Capita': [75, 81, 60, 52, 53, 51, 46, 46, 55, 39, 31, 42, 40, 47, 48],
    'Life Expectancy': [82, 84, 81, 83, 82, 83, 81, 82, 83, 85, 83, 81, 83, 82, 81],
    'Education Index': [95, 88, 92, 95, 93, 94, 93, 92, 92, 85, 85, 90, 88, 89, 91],
    'Happiness Score': [76, 75, 78, 75, 74, 73, 70, 72, 73, 59, 58, 70, 66, 69, 71],
    'Innovation Index': [68, 67, 58, 55, 58, 63, 87, 61, 46, 54, 64, 59, 54, 50, 45],
    'Environmental Score': [78, 81, 78, 68, 76, 78, 77, 72, 60, 65, 63, 58, 80, 73, 79]
}

data_matrix = np.array([data[key] for key in data.keys()]).T
corr_matrix = np.corrcoef(data_matrix.T)
mask = np.triu(np.ones_like(corr_matrix, dtype=bool))

fig, ax = plt.subplots(figsize=(10, 10))
masked_corr = np.ma.masked_where(mask, corr_matrix)
im = ax.matshow(masked_corr, cmap='RdBu_r', vmin=-1, vmax=1)

for i in range(len(data.keys())):
    for j in range(len(data.keys())):
        if i >= j:
            corr_val = corr_matrix[i, j]
            ax.text(j, i, f"{corr_val:.2f}", ha='center', va='center', color='black', fontsize=10, fontweight='bold')

ax.set_xticks(range(len(data.keys())))
ax.set_xticklabels([key.replace(' ', '\n') for key in data.keys()], rotation=45, ha='left')
ax.set_yticks(range(len(data.keys())))
ax.set_yticklabels([key.replace(' ', '\n') for key in data.keys()])

cbar = fig.colorbar(im, ax=ax, fraction=0.046, pad=0.04)
cbar.set_label('Correlation', rotation=270, labelpad=15)

ax.set_title('COMPONENT RELATIONSHIPS\nHow dimensions correlate with each other', fontsize=14, fontweight='bold', pad=15)

plt.tight_layout()
plt.show()

3.6. Alternative: Clustered scatter matrix

import matplotlib.pyplot as plt
import numpy as np

# Same data as above
countries = ['Norway', 'Switzerland', 'Denmark', 'Iceland', 'Netherlands', 
            'Sweden', 'Germany', 'Canada', 'Australia', 'Japan', 'South Korea',
            'United Kingdom', 'France', 'Belgium', 'Austria']

gdp = [75, 81, 60, 52, 53, 51, 46, 46, 55, 39, 31, 42, 40, 47, 48]
happiness = [76, 75, 78, 75, 74, 73, 70, 72, 73, 59, 58, 70, 66, 69, 71]
innovation = [68, 67, 58, 55, 58, 63, 87, 61, 46, 54, 64, 59, 54, 50, 45]
environment = [78, 81, 78, 68, 76, 78, 77, 72, 60, 65, 63, 58, 80, 73, 79]

# Create regions for coloring
regions = ['Nordic']*6 + ['Western Europe']*5 + ['Asia']*2 + ['Anglo']*2
region_colors = {'Nordic': '#2E4057', 'Western Europe': '#048A81', 
                'Asia': '#F18F01', 'Anglo': '#C73E1D'}
colors = [region_colors[region] for region in regions]

fig, ((ax1, ax2), (ax3, ax4)) = plt.subplots(2, 2, figsize=(14, 12))

# Four key 2D relationships
plots_config = [
    (ax1, gdp, happiness, 'GDP per Capita', 'Happiness Score'),
    (ax2, innovation, environment, 'Innovation Index', 'Environmental Score'),
    (ax3, gdp, innovation, 'GDP per Capita', 'Innovation Index'),
    (ax4, happiness, environment, 'Happiness Score', 'Environmental Score')
]

for ax, x_data, y_data, x_label, y_label in plots_config:
    scatter = ax.scatter(x_data, y_data, c=colors, s=100, alpha=0.7, 
                       edgecolor='black', linewidth=1)

    # Add trend line
    z = np.polyfit(x_data, y_data, 1)
    p = np.poly1d(z)
    x_trend = np.linspace(min(x_data), max(x_data), 100)
    ax.plot(x_trend, p(x_trend), "r--", alpha=0.6, linewidth=1.5)

    ax.set_xlabel(x_label, fontsize=11)
    ax.set_ylabel(y_label, fontsize=11)
    ax.grid(True, alpha=0.3)

    # Add correlation coefficient
    corr = np.corrcoef(x_data, y_data)[0,1]
    ax.text(0.05, 0.95, f'r = {corr:.2f}', transform=ax.transAxes, 
           bbox=dict(boxstyle='round', facecolor='white', alpha=0.8))

# Overall title
fig.suptitle('MULTI-DIMENSIONAL RELATIONSHIPS: 2D Projections of 6D Data\n' +
            'Pattern: Nordic countries cluster consistently across dimensions', 
            fontsize=16, fontweight='bold', y=0.98)

# Legend
handles = [plt.scatter([], [], c=color, s=100, label=region, edgecolor='black') 
          for region, color in region_colors.items()]
fig.legend(handles=handles, loc='center', bbox_to_anchor=(0.5, 0.02), ncol=4)

plt.tight_layout()
plt.subplots_adjust(top=0.92, bottom=0.08)
plt.show()

3.7. Discussion

Looking at the above graph:

What are the signifiers ?
What are the signified ?
What can we conclude from those graphs ?
How do they compare in terms of readability and visual unity?
Big findings? Are we this sure ? (For some heatmap values from 3.4, once the economical context of those countries is known, the analysis is pretty clear. But for some others, it's not so obvious.)

4. Visual Variables

This part of the lecture is available here: Visual Variables.

5. Graphic Rules and Grammar

5.1. Problem Construction

Any graphic is a solution to multiple possible ways to encode the same dataset—the “graphic problem” is to choose the most efficient/legible.
Design must account for perceptual tasks (lookup, comparison, grouping, pattern search).

5.2. Grammar of Construction

Density: Avoid excessive clutter, but enough detail for insight.
Retinal Legibility: Variables should combine without creating confusion.
Layering/Separation: Different elements must remain perceptually separable (via color, value, or shape).